While researching Anglo-Saxon board games, I came across the following book which is one of the key sources for reconstructing the ancient game of tabula (an early form of backgammon) as played by the Greeks and Romans. The author carefully analyses Agathias’ epigram 482 and other sources. I could not find the text in English so used a popular web service and my ‘O’ level French to produce a very rough translation of chapter XVII, which I offer below. If anybody would like to help improve this text, please get in touch!
Title: Les jeux des anciens : leur description, leur origine, leurs rapports avec la religion, l’histoire et les moeurs / par L. Becq de Fouquières; ouvrage accompagné de gravures sur bois d’après l’antique, dessinées et gravées par M. Léon Le Maire
Author: Becq de Fouquières, Louis (1831-1887).
Publisher: (Paris)
Publication date: 1869
The book is out of copyright and an OCR version of the French text is available on this website:
https://gallica.bnf.fr/ark:/12148/bpt6k110685x/f368.item
Becq de Fouquières approached his analysis as a player of tric-trac, a game commonly equated with backgammon but in fact significantly different, though played on a similar board (the tric-trac board has additional holes to score points within a game). In trictrac, counters are not removed and re-entered during the game. Instead, points are scored throughout the game based on the configuration of the pieces and dice, with bearing your ‘dames’ off first being only one of several ways to score points. Isolated counters give your opponent an opportunity to score points. A game is won by being the first to reach twelve points. On scoring a ‘trou’, that is winning a game, the player can either reset their opponent’s score to zero and continue this game, or they can reset the game and start a new one.
When Austin later based his interpretation on Becq de Fouquières work, I don’t think he realised how much difference this can make to the reconstruction of the rules.1
When classical writers refer to counters going back, do they mean the reset of the scoring counter (trictrac), the reset of the game (trictrac) or a game counter having to reenter the board (tric-trac)?
Translation notes:
The word ‘tablier’ is commonly translated as ‘apron’ and that’s the word used below, but according to some websites, ‘tablier’ can also mean a rigid panel or board, which seems more appropriate in this case, echoing the Viking phrase “to play at tables”.
The Greek quotations have been replaced with “greektext” because they have not been correctly read by the OCR. I hope to fill in this missing text at some point.
Becq de Fouquières calls the game counters ‘dames’, here translated as ladies or queens; this is trictrac usage.2
The terms ‘grand jan’ and ‘petit jan’ are from trictrac.
THE GAME OF TWELVE LINES
Apart from games of chance, which we have just spoken of, and games of combinations, which we shall deal with in the following chapters, the ancients knew a game in which chance and combination played a role in turn. The Romans called it the game of twelve lines (ludus duodecim scriptorum). It has been preserved until us without much modification and after having worn the game name of the apron for a long time, it is more generally known today as tric-trac.
When starting the study of this game, it is first of all a very important remark to make, which is that the Greek writers who spoke of it did not give it a special name which would make it distinguish a priori from the other games of chance. They simply call it a game of dice (greektext), and it is only by developing their thinking and the context of the sentence that we can be sure that it is not the game of dice itself that is, but the particular game which has become our tric-trac. Thus, five hundred years after J.-C., Agathias, who left us an epigram on a game of tric-trac of the Emperor Zeno, where this game is described in enough detail for us to cannot be mistaken, simply referred to the game in which Emperor Zeno was entertained by the expression of “a game of dice (greektext).” This is worthy of attention. He does not translate the Roman name of the game (ludus duodecim scriptorum), because this way of saying was not used among Greek writers, nor does he give it the Greek name (greektext) by which almost all modern scholars have wanted to designate it. This would already tend to make us suspect that it is too generally accepted an error to see diagrammism as the ancient game of tric-trac of the Greeks. We will come back to this question later. However that may be, we can observe, by this example and by others which will follow, that the Greek writers, when they designate this game, only use the very general term of game of dice.
Let us therefore see from a few passages the inductions that it will be possible for us to draw, both on the character and on the progress of the game. Plato, in Book X of the Republic (Ed. Bekker, tom. VI, p. 484), has spoken of it in a few very remarkable lines, where he establishes that law and reason must react against pain. Affliction, he says, is an obstacle to what should be done in these meetings. What should we do then? Deliberate (greektext) on what has just happened and as in the fall of the dice (greektext), put down your things after the dice thrown (greektext) according to the means that reason will have demonstrated the best. »We can compare this passage from Plato with another from Plutarch, in the life of Romulus (v). In it he tells a story to which we have already alluded, that of the priest who plays dice with Hercules.
Plutarch here alludes to tric-trac (we use this modern word for clarity and conciseness), because after saying that the minister invites Hercules to play dice with him (greektext), he adds: pieces for the god, then for him (greektext) a remarkable expression reminiscent of Plato’s.
Thus, we can now have a rough idea of the nature of the game at three successive moments. You have to: First, roll the dice (greektext) second, deliberate on what to do (greektext); third, to place the pieces (greektext) and, of course, as Plato says, employing the nuance of medium, to place them in view of its interest (greektext), From this third expression we can deduce the term by which the Greeks designated the position of the pieces (greektext), a term that in fact we find in the epigram of Agathias, when he describes the variously combined position of the pieces (greektext).
Two other passages from Plutarch confirm what we have already said. The one, the most important, is in the life of Artaxercès (xvii) “Parysati s, mother of Artaxercès, he says, was skilled at the game of dice (greektext). So there is no doubt about a man skilled at tric-trac the Greeks simply said he was skilled at playing dice. “She favored,” continues Plutarch, “the debauchery of the king. One day she suggested that he play a thousand darics at dice. She lost and paid. She then proposed to him to play a eunuch to be chosen among those they had, five except at the will of each one. This time taking care of her game (greektext), and the dice for that matter falling well for her, she won, took Masabate and had him put to death. “
From yet another point of view this account is instructive. It is clear that in writing the life of Artaxercès, Plutarch used local traditions or oriental manuscripts, this passage therefore shows us at a remote time the widespread use in Persia of the game of tric-trac. Indeed, since the highest antiquity, this game seems to have been known to the Persians.
One can consult on this subject the treatise of the Eastern Games of Hyde, where it is said that in all the East this game was known by its Persian name of Nerd, term which indicates a kind of small elongated cylinder which one placed upright on its base. And Hyde testifies to the habit which Orientals have of using, not round and flat pieces like our ladies, but small cylinders erected and worked at their end in the form either of a dog’s head or of a lion’s head. This usage did not contribute little to confusing another Greek game, called the Cities which we will discuss later. In this game the Greeks seem to have used as pieces small figurines of dogs, which they had doubtless borrowed from the East; and from there it was concluded that the game of Plinthion or Cities was nothing other than the game of tric-trac, which is in my opinion a very serious error. The Greeks may have modeled their dog after the Persian Nerd, but the game they used was by no means tric-trac; for the latter one used pieces (greektext) which were undoubtedly flat and which the Romans properly called small stones, calculations (calculi).
Let us return to Plutarch. He says in the life of Pyrrhus (xxvi), that Antigone and compared Pyrrhus to a dice player (greektext) who often brings good shots but who does not know how to take advantage of them. “
This passage adds nothing to our knowledge of the game; however, there is further evidence that a dice player was simply called a tric-trac player.
We must still note another expression of Plutarch, which is found in his treatise On the tranquility of the soul (v) Plato, he said, compared our life to the game of dice (greektext), where it is necessary that the dice say well and that the player uses well the die which will be due to him. Now, from these two points, the event and the fate of the dice are not in our power; but to receive gently and moderately what pleases fortune to send us and to assign to each thing a place (greektext), where it can profit a lot if it is good, or harm little if it is bad, that is in our power if we are wise. II We saw earlier that it was necessary to throw the dice, deliberate, and then place the pieces. Plutarch tells us here what this third operation consists of, that is, to assign a place to each piece, that is to say to distribute the pieces in the squares in the most advantageous way.
So, by sticking to the only authorities that we have just mentioned, we can easily determine the general principle of the game. It consists in translating on the table, by the advancement of the pieces, the numbers brought by the dice and since this advancement is determined by a number that cannot be changed, good play must consist in choosing which pieces are to be set in motion by which dice with more profit than others. We will soon see in the epigram of Agathias how the position of a coin could be profitable or harmful.
Note that the table on which the pieces are moved is only a counting table since, at any time in the game, we can, by a series of successive additions, by summing the spaces traversed by the pieces, obtain the total of the points brought by the dice. It was therefore with good reason that the Greeks simply called tric-trac a game of dice, since, to use an unusual but very clear expression, it was only a game of dice to write, where all the skill consisted in the manner of scoring the points. In addition, as the highest number marked on the dice is six and therefore the apron is a calculation table to be used to transcribe the additions of a sort of numeration by six, it is natural to think that its divisions will be in correlation with this numeration, and, for ease in the calculations, divided into series of six by means of some separation. We can already predict what this table will be.
The last work in which this game was mentioned is that which Christie published in London in 1801 under the title of Reclierclies on the ancient Greek game invented by Palamède (An inquiry into the ant. Gr. Game inv. By Pal .). This game is Pettie. Christie, in our opinion, has very skillfully reconstructed it; but then he fell into a frequent error which consists in reducing everything to the same absolute and unique type. I do not share Christie’s ideas in this regard at all and when he wants to prove that the tric-trac apron is only a modification of the five-line checkerboard of the Pettie, my reason refuses to follow him on this ground. And to mark in a word what separates us, I would say that Christie sees in the construction of the table the basis of the game, while for me the principle and the starting point of the game is the dice and its six faces.
This is why in my opinion the Greeks were logical in the choice of the term with which they designated this game, which was really only a game of dice. I insist on this because this point of view is, I believe, new at least neither Hyde, nor Meursius, nor Bulengerius, nor Sentflebius, neither Supported, nor Calcagninus have seemed to perceive it.
Thus, the apron with its sexesimal divisions has its origin in the six faces of the dice, so that if the ancients had known only the eight-sided dice we would have an apron with octoseimal divisions, and that if after having for centuries used the eight-sided dice they had come to discover and adopt the six-sided dice, the apron, which is only a counting table, would certainly have changed, just like our barometers, our graduated circles, etc., had to change the number of their divisions, when the duodecimal system was succeeded by the decimal system. In the game of tric-trac the apron and the dice are constructed according to a sexesimal system.
We can already see the numerous inductions which have enabled us to draw some information borrowed only from two writers of antiquity, from Plato and Plutarch. We will come back to the Greek writers, but later because then it will be about information provided by writers of the Lower Empire. First, it is necessary to examine what the Latin authors can teach us.
Everything leads us to think that the apron saw its shape change slightly when the game passed from the Greeks to the Romans. When the Greeks want to designate the apron it is remarkable that they use expressions which do not indicate a particular shape. For them it is only a plate (greektext) a planchette (greektext) and there is nothing to suggest that their apron had this honeycomb shape that the Romans had undoubtedly borrowed from the East. The Greeks did not have a term that exactly corresponded to the Roman name (alveus, alveolus) and writers of the Lower Empire retained the custom of designating the apron only by the general term of table (greektext). The Romans also used it, but to designate indifferently the table which was used for games of chance (Festus: tabula aleatoria) and that which was used for games of combinations (Martial: labula lusoria).
There is a very curious monument of antiquity of which we must speak here. It is a game table found, a long time ago, in Rome in a public swimming pool and which has been published several times, among others by Saumaise in his edition of the writers of the August History, by Gruter in his Monumenta Christianorum (p. 1049, fig. I) and more recently by Christie. This table which we are going to put before the reader’s eyes deserves to fix our attention for a moment. It is not at all a Roman apron (alveus) it is a real Greek apron (greektext), flat, without rim; it bears an inscription rather carelessly traced by an unskilful hand and which unrolls irregularly above and below a Greek cross. Here it is as it was read in ‘To the dice players Jesus Christ gives assistance and victory to those who trace his name even when they are playing dice. “

On first inspection of this table, it is evident that the worker who built it had only very imperfect notions of the game of tric-trac. Without counting the lines that form the frame, we find twelve, but they are clumsily divided into two unequal parts, seven on one side, five on the other. The worker knew the general appearance of these gaming tables, the number of lines which the Latin title (ludus duodecim scriptorum) sufficiently indicated to him, but he was unaware of the other details of the game, such as the separation of the twelve. lines in two equal parts of six lines each. However, it is remarkable that he chose a marble table, flat like those which were undoubtedly in use in Greece, and that he gave the game its Greek name, since we find in the inscription the expression of play dice (greektext). Rich, in his Dictionary of Antiquities, gave this table after Christie, but he did not reproduce the vicious arrangement of the lines.
It is quite evident to us that the worker was a very bad tric-trac player and a very good Christian. He was undoubtedly a member of religious associations and seems to have been very versed in the details of the religion there are many indications of it the Greek cross, the inscription itself, below the cross the two symbolic triangles and finally, a very curious detail, a voluntary spelling error (greektext), which was dictated to him by the desire to include above the cross the two symbolic letters omega and alpha. But this table was only a means of proselytism, tempting the superstition of the peasant players who, by the hope of victory, would decide to trace the name of Christ, the first concession and the first step made towards the new religion.
The two most remarkable points for what concerns us here are first of all the title which the Greek worker gives to the game and then the construction of the apron on a flat stone according to the custom of his country.
The Romans very early made use of aprons in the form of honeycombs. One of the oldest testimonies which remain to us is a fragment of Lucilius (xiv, 4) quoted by Priscian (VI, v) a It is possible for you, I say, to calculate the chances of Naumachia as well as of the apron and ladies (alveolumque putare and calces). Thus the apron in the Romans bore the name of alveolus (alveolus) and the token or the lady, that of calculus (calx, primitive form of calculus). And there is no mistaking it, it is indeed the play of the twelve lines that Lucilius has in view, because the same expression (alveolus) is found in Aulu-Gelle (I, xx) “What geometers, he says, call dice presents a square on all sides. Such, says Varro, are these dice (tesserœ) with which one plays in the alveolus (in alveolo). The Romans also sometimes used the more general term of table (tabula) which is none other than our word apron. Martial (II, xlviii) said “An apron and ladies (tabulamque calculosque), a few selected books, and I give you all the delights of the baths of Nero.”
The expression of alveolus is not the most frequent, moreover. The apron most often takes the name of alve (alveus). In a passage identical to that of Aulu-Gelle, Vitruvius (V), after having described the shape of the cube adds “Such are the dice (tesserœ) that when playing we throw in the apron (in alveo).
The alve is properly a trough whose edges prevent the dice and checkers from falling. And I will point out here an error of Rich (with the word tabula) He says that one threw the dice on a table and that one executed the blows on the apron. No authority can allow him to advance this, while the above passage from Vitruvius is categorical one threw the dice in the apron.
Pliny (XXXVII, n) has preserved the dimensions of the apron for us. “In his third triumph, Pompey, he tells us, carry a game table (alveum lusorium), with its dice, made of two precious stones, three feet wide and four long. In this table there was a golden moon weighing thirty pounds. We will come back to this moon in question here later. This tric-trac table came from Asia; It is therefore from the East that the Romans very probably borrowed the alveolar form of their aprons. As for the dimensions, all could undoubtedly not have the same as that of which Pliny speaks; but it is probable that the width was always with the length in the proportion of 3 to 4.
The ancients used wood or the most precious materials for aprons and dice. Pliny has just told us about a table made of two precious stones; Petronius (XXXIII) describes a table of terebinth and crystal dice to us. “Will you allow me to finish my game?” A child followed with a table of terebinth (tabula terebinthina) and crystal dice (crystallinis tesseris); and I saw the thing in the world that announced the best taste instead of white and black ladies (pro calculis albis ac nigris), he had gold and silver denarii. »Thus, as today, we used checkers of two colors, and we were right to say that the pieces of the game of tric-trac were. flat, for we see that they were replaced by gold and silver denarii.
We built aprons which, on the one hand, were used for the game of twelve lines, and on the other, for the game of latroncules. This is what an epigram by Martial explains to us (XIV, xvii) “Here, the die and its six point are marked twice; there, a pawn perishes under the efforts of two enemies. The second line relates to the game of the latroncules, and the first to the game of the twelve lines. I may understand this epigram a little differently from other translators. We must not lose sight of the fact that it is not the dice he describes, but the table; and it is to the twelve lines, or better to the two times six lines that he alludes, by saying here, twice the point of six of the dice can be counted; and this interpretation returns to what we said above, that the starting point of the game was the dice, with its six faces and its six points. Travel aprons were also made. This was the one Claude used, passionate, as we know, for gambling. “He even played while traveling,” says Suetonius [Cl. XXXIII); his car and his table (alveus) were arranged so that the game did not get mixed up. “
Finally, let us add that a cone was used to shake and throw the dice, and a tower (greektext, turricula); we have already said that this tower was a cylindrical cornet pierced at both ends, inside which were steps that the de-rocks tumble down as they fall. Moreover, sometimes the cornets themselves had degrees which made the use of the tower almost useless; one has been preserved which Boldetti published, and which was reproduced in the Dictionary of Christian antiquities of the Abbe Martigny, after which we had this engraved.
Until now, we have seen in Latin writers only allusions to the apron, its shape, its material, as well as that of the dice; but, as in the Greek writers, one does not fail to find there also allusions to the nature and to the general progress of the game. It is fortune, said Petronius (LXXX), which regulates friendship, as it is chance which regulates the walk of the lady on the apron. “The thought of Terence (Adelph. IV, vis) is more famous, and above all higher” Human life is like dice (tesseris) if the necessary point does not fall, then art must correct what the fate sent us. In this passage Menander’s influence is visible.
Terence borrowed from him until the expression, because he calls this game the game of tessera (which is the greektext of the Greeks).
We have not yet, as we have noticed, encountered the trace of the Latin name (ludus duodecim scriptorum). The Romans had three ways of designating this game: First, the expression borrowed from the Greeks, as in Terence, the tessera game second, the expression of playing apron and checkers, used by Valère Maxime (VIII, viii) “Scévola,” he said, “gave a few moments to the game of the apron and the checkers (alveo et calculis). And finally, third, they referred to this game by the number of lines drawn on the deck. This is how Ovid (Art d’aimer, III, 364), paraphrased the title of the game in a passage that remained obscure for a long time. He enumerates various games in which he advises a young girl to indulge; after those of latrines and solitaire comes the one in question here. “It is,” he said, “a kind of game where on the table are drawn as many divisions as there are months in the rapid year. This is the game of twelve lines.
Here are now two passages, one from Quintilian, the other from Cicero, where it is expressly named the game of twelve lines. Quintilian (XI, ii) alludes to Scévola’s taste for the game, and tells a fairly naïve story as proof of his prodigious memory. twelve lines (in lusu duodecim scriptorum), part where the first he had advanced a lady (quum prior calculum promovisset), returned on returning to the countryside all the disposition of the game, and full of this memory, returned to his opponent who agreed that everything had happened that way. ” The story is quite naive, in fact, in that, without paying attention, Quintilian supposes that Scévola’s opponent has an equally prodigious memory. So this passage gives us first the title of the game (ludus duodecim scriptorum); and then the term which means to carry a lady forward (promovere calculum), however this is only a general expression, it is Cicero who will teach us the technical term (Fragm. Hortensius).
This is a convention that Cicero makes with his interlocutor; he will allow him to come back to a reasoning that he might regret having expressed I grant you, he said, what we have customary to play in the game of twelve lines (in duodecim scriptis), to resume a queen (ut calculum reducas) if there is one that you regret having played (si te alicujus dati pœnitet).
Earlier we saw the general expression of carrying a lady forward (promovere calculum) here Cicero gives us the exact term to play, to place the queen (dare calculum), and also the opposite term to take back a lady , to bring it back (reducare calculum). At the same time he gives us a rule of the game. Among the ancients, chance immediately ceased to throw the dice; the game therefore belonged to the skill, there was no surprise. Even after having played a queen (dare calculum) it could be taken back (reducare calculum) to replay it. This expression of bringing back a queen is obviously equivalent to that of replaying a queen. The Latin term to play a lady (dare calculum) translated the Greek term (greektext), and the term to replay (reducare) corresponded to the Greek expression to replace a lady (greektext) that Suidas has preserved for us.
This fragment is very valuable, and enables us to explain two passages from Ovid which, despite the very correct remarks of Hyde and other commentators, are most of the time poorly rendered by French translators. The first is in the Art of loving (ii, 203). The poet advises the lover to please his mistress in everything, even to use deception so that she has superiority in all things. Will she play and throw with her hand the ivory numbers (eburnos numbers), that is to say the dice, you, throw badly (tu male jactato) and play badly the point brought by the dice (tu male jacta dato)
First, why does he advise the lover to throw the dice badly, when we know that the fate of the dice depends only on chance? Note that the poet supposes the case where the lover and his mistress will play with the hand (manu) and not with a cornet, the purpose of which is precisely to make cheating and trickery impossible. Once the dice have been thrown, he advises her to play badly (male dato), that is to say to place her checkers badly; and here we find the expression that Cicero gave us to be born.
The second passage is in Les Tristes (II, i, 475) it has remained perhaps more obscure. Ovid enumerates the treatises composed on games of chance there. “One can learn there,” he says, “the points marked on the dice and how, the game to be played being called (distant vocato), it is advisable to throw the dice (millere tesseras) and to play the blow (dare). This passage is very remarkable in that Ovid alludes in it to a rule to which any somewhat skilful and thoughtful player must adhere. What does he mean by this expression the distance being called (distante vocalo)? What he has in view is precisely the work of the mind, which, in any tric-trac player, must precede the action of touching a queen and even of throwing the dice, a work which often takes place. done aloud, when a player, cone in hand, while shaking his dice, considers the position of the game, calculates and calls out the points he could wish to make this or that lady cross the distance which will put her in a better or less bad situation.
This is almost all the information that Latin writers have given us on the game of twelve lines. We must now study the most considerable and the most curious monument that antiquity has left us on this game, it is the famous epigram that Agathias composed on a game of tric-trac by Emperor Zeno (ix, 482).
From cover to cover it is full of details that are precious to us. Until today she had not been explained in a satisfactory manner. Jacobs declares it obscure; and De Paw, who made it the subject of a particular dissertation (De alea veter, ad ep. Ag., Traj. ad Rh. 1726, in-8 °), could not give a solution. The scholar Hyde and Christie were no happier. The solution is, however, very easy and very simple, as the reader will judge.
Here is first the translation I pass the first verses which are only a philosophical reflection: One day Zeno, king and protector of the city, finishing a game with the dice full of mysteries, was surprised by a variously combined position of the pieces which was such (greektext) him going from white (that is to say from the white ladies’ hut) towards the back road (greektext) the sixth hut had seven ladies, the ninth only one. The extreme box (greektext by implying greektext) had two ladies like the tenth. The one following the extreme box (greektext) had two. Finally the divine hut had another unique and last lady. The blacks had left two ladies in the eighth fret (greektext) and as many in the eleventh. Two ladies shone in the twelfth and only one rested in the thirteenth. A double coin adorned the Antigone. The same mark was seen in the fifteenth as in the eighteenth. There were two more ladies in the fourth from the last. The king who had fallen the command of the whites, not foreseeing the trap which he had in front of him threw without thinking of it with his cone three dice which disappeared in the staircase of the wooden tower (greektext). He brought in two, six and five, and immediately the eight ladies who had just joined together were split into two. “
Agathias thus gives us the respective position of the pieces of each player. Each of them had fifteen pieces which made a total of thirty pieces, fifteen of which were white and fifteen black. He us further says that Zeno played with three dice and since we have no other evidence of the number of dice the Greeks used, while we know that the Romans took only two, we must conclude that probably the The game of two dice was in the Roman habits and that the game of three dice seems to have been preserved in Greek customs. It is, however, very probable that when it was imagined that only two dice would be used, the game would have to undergo some modifications. The ease of scoring points by beating open checkers necessarily diminished; but the game was complicated by the rules relating to taking possession of the corner and the action of filling the small and large jan.
What was the goal of each player? You had to run your ladies through the twenty-four boxes of the table and then probably take them all out of the apron. But, as happens in our tric-trac, we did not always push that far. While making his queens march forward, we tried to cover them, and to make them occupy successive squares so as to bar the path of the other player, we beat the opponent’s queens and each time we scored points. It is also probable that one counted by holes, a hole worth a certain number of points, twelve certainly, and constituting a gain definitively acquired, while the points were distinguished when the adversary made a hole. We will see how, from the epigram of Agathias, all its consequences are deduced naturally.
The direction each player takes is explained to us by the sentence of Agathias, in which he gives us the position of Zeno moving from white to the posterior road (greektext). From this, we see that box 1 took the name of white box (greektext), that is to say box where we put the white ladies; while box 24 was called the black box (greektext), that is to say box where we put the black ladies. The road that his ladies had to take was called the road (greektext) it was divided into two parts, one from 1 to 12, the other from 13 to 24.
As the one who had the white ladies was supposed to have the place of honor, it was white ladies that the road was supposed to descend, as from upstream to downstream and, relative to the player who had the white ladies, the road divided. in two parts the first, the anterior route (greektext), going from 1 to 12 the second, the posterior route (greektext), going from 13 to 24. So that Zeno, as Agathias says, went from the hut of white towards the back route (greektext), while his opponent went from the quarter of the quarter towards the previous route (greektext). This is what I think Christie did not understand.
One last note: it is obvious from this example that the cornet (greektext) is very different from the tower (greektext), since the dice fell from the cornet into the tower which had, as the poet says, degrees than the dice. tumbled down.
Let us now seek the explanation of this epigram. To arrive at the solution it suffices to proceed mathematically by going from the known to the unknown.
We can without hesitation place the ladies whose position Agathias gives us by the number of the box. Thus, for white, we will easily place seven queens in the sixth fret, one in the ninth and two in the tenth. For quarter notes, we will put two in the eighth fret, two in the eleventh, two in the twelfth, one in the thirteenth, two in the fifteenth, two in the eighteenth and two in the twenty-first, which is the fourth from the last. It remains for us to determine for the white ones, the place of two ladies that Agathias says occupy the extreme box, of the two others who occupy the box after the extreme one and of a last lady placed in the divine box; for black, the position of the two ladies occupying the Antigen box.
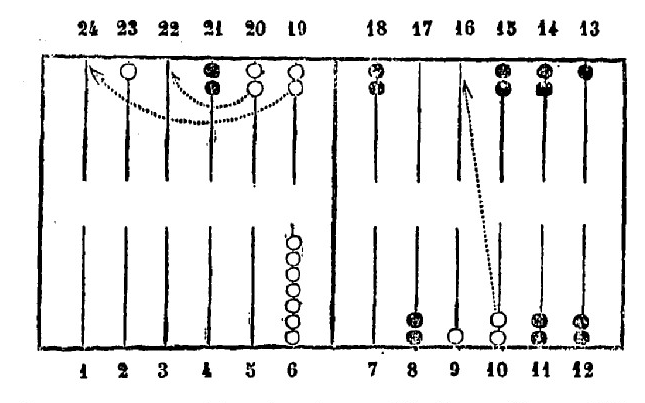
Let’s start by determining Antigone’s box. Let us first pose the essential condition that the emperor must necessarily be obliged to discover his ladies. Now, notice that if square 14 was not occupied, Zeno, bringing two, six and five, could, for example, take one of the queens from square 10, bring it by six to square 16, and cover it, by five and two, by means of the queen in square 9. The number of her covered queens would not be changed, which cannot be. Therefore, square 14 must be occupied, and as we only have two black checkers left to place, we must put them in square 14, which will thus take the name of Antigone square. So far no difficulty Hyde and Christie must have reasoned in the same way, since they arrived at the same result.
All the black ladies being placed let’s move on to the white ones. Since square 10, the extreme square and the square after the extreme each have two queens and Zeno must necessarily be forced to discover them by the three numbers two, six and five, it is therefore necessary that the queen unique and last, that Agathias says placed in the divine box, occupies a position such that Zeno cannot play it, since if it were possible for him he would avoid discovering one of his ladies, which cannot be. A queen placed in square 23 perfectly meets all the conditions of the problem, square 23 will therefore be the divine square.
Let us now determine the position of the extreme fret and the fret after the extreme. It is especially here that my solution differs completely from those proposed by Hyde and Christie. The whole difficulty lies in what the extreme box (greektext) was. Hyde places it in square 1, and the one after the extreme (greektext) in square 2. It is impossible, since in this case Zeno would cover the queen of square 9 by six and two, would put an eighth queen at square 6 by five and would thus have more checkers covered than it had before the stroke. Christie, for his part, places the extreme box in box 24 and is then obliged to put the box after the extreme in box 23, which goes against the meaning, since box 23 is not the box after the extreme, but the one before the extreme. He further assumes that at this end of the table the game should start to turn again in the direction 23, 24,1, 2, 3, etc. But by admitting for a moment the position imagined by Christie, we see that Zeno could, among other ways of playing, take one of the two queens from square 23 and come by six and five put it in square 10 and then play by gods. the other queen from square 23 to square 1. He could still occupy square 1 by two and come and occupy square 5 by six and five, by means of two queens who would therefore be said to be covered.
We see that in the different solutions proposed by Hyde and by Christie, Zeno would have to his choice several ways of playing, by means of which he would avoid having his eight queens discovered, which goes against the very conditions of the problem.
It’s because Hyde and Christie were completely wrong about what the extreme box is. Now, from my point of view, here is what it is that this box is the furthest away, the highest (greektext, summus) to which a lady can reach by means of the highest possible point. In short, it is the square with the longest range, and as the Greeks played with three dice, it is the furthest square, the highest to which, all the checkers being crammed at the beginning on square 1, a queen can at a pinch reach by the strongest throw of the dice which is that of the triple-six. The queen thus taken in square 1 would jump by six in square 7, by six again in square 13, and a third time by six in square 19. Square 19 is therefore the square with the longest range. the highest box, the extreme box (greektext) and box 20 will therefore be the box after the extreme (greektext).
If I have reasoned correctly, the pieces being placed as I said, Zeno bringing two, six and five must be forced to uncover his ladies. Now, there is no other way to play move two, six and five than to transport one of the queens from square 10 to square 16 by six, one of the queens from square 19 to square 24 by five, and one of the queens from box 20 to box 22 by two.
I will add to prove the excellence of this solution, that it fits well in the spirit of the epigram; for we see that very great importance was attached to covering the ladies, evidently to prevent them from being beaten. Now, the epigram presents to us the position of the pieces of the two adversaries as remarkable, in that Zeno was far from foreseeing the trap set under his feet; and, in fact, the pieces being placed as I have explained, Zeno must have thought that he could play in complete safety, since, out of the fifty-six combinations that three dice can provide, fifty-five were more or less favorable to him, while only one was entirely unfavorable to him.
Now, this unique combination was precisely two, six and five. Agathias has thus contrived to versify a sort of little tric-trac problem; and he exposes to us in his epigram an arrangement of pieces, such that, out of the fifty-six possible combinations of the dice, only one must necessarily put the pieces in the most unfavorable position.
It is easy to show how the position of Zeno, good as it was, indeed becomes disastrous after the roll of the dice gods, five, six. Suppose, which we are allowed, that the game is in twelve holes, each hole worth 12 points, and each queen beaten bringing a gain of two points, according to the rules of our tric-trac. Suppose again that before throwing his dice, Zeno has 11 holes and 10 points, and that his opponent has only 9 holes and 8 points. Zenon, considering his position while waving his dice, must indeed be full of hope; for his opponent has a queen discovered in square 13, and to beat her, that is to say to win the game, it suffices to bring a three or a four, or the combination of six and one. However, out of the fifty-six possible rolls of the dice, forty win. On the sixteen others, five do not make him discover any lady, ten force him to discover one, two or three ladies, only one (two, five and six) obliges him to deliver five discovered ladies to the enemy. Thus forty throws of the dice win him; fifteen gave him hope, either to win the next move, or to keep a relatively good situation; only one puts him in the case of losing the game all at once. Because if his opponent, after having scored for the queen 13, beaten by two and five, the two points which give him 9 holes and 8 points, brings one, two and four, he will beat the queen 9 by ten points, the queen 10 with ten points, queen 16 with four points, ladies 19 and 20 each with two points, in all twenty-eight points which, added to 9 holes, 8 points, will complete his twelve holes and make him win the game.
The careful examination of the position of the queens of Zeno and of his opponent may still suggest some conjectures on the progress of the game. The occupation of square 13 by a single queen is particularly remarkable. In our tric-trac, this corner can only be occupied by two ladies that one die rolls simultaneously; and one can only abandon this position by removing the two ladies at the same time. This rule, we see, did not exist in the ancient game. However, it seems to have been established with the aim of increasing the difficulties that a player can to meet to fill his big jan we can therefore conclude that in the game of twelve lines, we did not seek, as in tric-trac, to fill with his ladies the six boxes of the small or the big jan that could and had to meet , but the player did not see the same importance as the tric-trac player, since particular advantages were not attached to it. Examination of the game of black checkers seems to support this view. It is visible that black was favored by a series of dice rolls which allowed them to place themselves regularly and to occupy five successive squares. Chance would therefore have helped to facilitate the occupation of the great jan for the blacks; but the two ladies still placed in square 21 make us suspect that the black did not try to take advantage of the facility that the dice offered them to fill the big jan, and that for the very probable reason that we do not did not attach any definite advantage to this operation. Thus, the game seems to have consisted only in knocking down checkers according to the dice out, in carrying them forward, while striving to bar the way to the opponent by occupying a series of successive squares, is to be marked. points each time you could beat an opponent’s queen.
Now, with three dice, the combinations by which one could beat a discovered queen, either directly or by correspondence, were much more numerous than with two dice, and the game thus had a certain speed, the unforeseen of which perhaps equaled. be the interest that the rules relating to small and large jan have since added to it.
It should also be noted that when examining the two games, that of Zeno appears to be the worst. The epigram of Agathias nevertheless gives us the position of the Emperor as very good as we have seen in fact that it was in relation to the hope which he could conceive; but this hope can only have its reason for existence if we suppose, as we have done, Zeno very near to the goal, that is to say, very near to winning. The game de Zeno, very bad in himself, is good only relatively to the few points he has left to do, or, in other words, to the great number of points he has previously scored; which leads us to conclude that each player, when he made a hole, had the right to go away, according to the term and the rules of our tric-trac, that is to say to restart the game by replacing all his ladies in the box which serves as their starting point. If in Indeed, we regard this rule of our tric-trac as one of the probable rules of the game of twelve lines; Zeno’s position can therefore be conceived as very good. For he may have played very well throughout the game, and at the moment when, for example, he had 11 holes, to go away, that is to say to start playing again from square 1. , when the dice turned against him. However, he was fortunate enough to manage to beat his opponent’s ladies by 10 points, and Agathias shows him to be in a position where he can hope to win, while on the contrary fortune is laying a trap under his feet.
I believe that I have sufficiently brought out what the game of twelve lines of the ancients and the game of tric-trac of the moderns have in common and what is different.
It only remains for me to add to what precedes a few considerations on the antiquity of this game and on its symbolic character. As for what concerns the invention of this game, we will not be surprised to see Pnlambdo, among the names of those to whom it has been attributed. All it took was a verse from Sophocles where it is said that Palamedes had found the dice (greektext) to be credited with the invention of the game of twelve lines. But it seems to me useless to agitate these insoluble questions unduly. Let us grant Sidoine Apollinaire, Lactance, Planude, as well as many others, whether it is Palamède. It doesn’t matter; There is no great interest in attaching to an invention thus lost in the mists of time, one name rather than another.
However, in questions relating to origins, we always see Hellenic self-esteem; to all things the Greeks liked to give a Greek origin. In tric-trac, therefore, a Greek inventor was needed, the name of Palamède was put forward and flew from mouth to mouth to us, who repeat some of these poetic lies very seriously. Now, it could well happen that the Greeks had received the first notions of this game from the East or Egypt. This origin pierces through a passage from Plato’s Phaedra (Ed. Bekker, tom. I, p. 96), where Socrates expresses himself as follows: “I have heard that around Naucratis of Egypt there existed one of the oldest gods, the one to whom is consecrated the bird called Ibis whose name is Theuth and that he was the first to discover number, calculation, geometry, astronomy, checkers and dice (greektext). ”It is in connection with this passage that Eustathe (p. 1397, 12) points out that the interpreters of Plato explain that the Pettie, to which Plato refers, is not the game played by the Greeks under this name, but another, by means of which the Egyptians represent the revolutions of the sun and the moon, as well than the elliptical movements of the stars.
We know the symbolic turn of the mind of the Egyptians gold, in the apron, in the twelve lines, in the cornet, etc., they saw a symbolic representation of the system of the world, as in the game of drafts they saw a symbol of the happy life that the righteous led after their death. It is this Egyptian legend that all the Greeks of the Lower Empire repeated.
Thus, Suidas says, to the word apron (greektext) “It is the name of a game invented by Palamedes, when the army of the Greeks was assembled. It is not without philosophical significance, because the apron (greektext) is the image of the Cosmos; the twelve boxes (greektext) are the twelve signs of the zodiac; the cornet to throw the dice in which appear the seven points (greektext, by adding the points of the opposite faces) are the seven planets; the tower (greektext) is the zenith, from which everything descends towards us, happiness and misfortune. “
Cedrenus repeats the same things almost identically. Isaac Porphyrogenet also says (Paralip. Hom.) “Palamedes is the first who imagined playing the apron (greektext). It was in accordance with the movements of the seven planets, whence, according to Fortune, come, it is said, to mortals all joy or pain, that he built the apron (greektext), that is to say the god table (greektext) representing the Cosmos; and, in correlation with the twelve signs of the zodiac that he constructed the twelve boxes (greektext), that is to say the entrenchments (greektext). “
All these ideas fit perfectly with the way of seeing the Egyptians. They also allow us to explain a passage from Pliny (XXXVII, ii), where it is said that Pompey, in his third triumph, made appear an apron four feet long and three wide, made of two precious stones, and in which was a moon of the weight of thirty pounds. We wondered what this moon was, and a translator of Pliny went so far as to claim that the apron was a chessboard and that this moon was the piece called the Queen. This moon, weighing thirty pounds, should have been about ten centimeters in diameter. metre. We. it is difficult to imagine a piece of this size in this alleged chessboard, it is pure reverie. Here is what it was most likely that this moon. Let us note first of all that it is a detail rather insignificant for him that Pliny repeats according to a saying, since he did not see him, not being yet of this world at the time of the third triumph of Pompey. Now, what he was told to be a golden moon was quite naturally only a golden ball; a crescent, moreover, would have represented the moon much better to all eyes than a ball. We know that in his third triumph, Pompey returned from Asia, which he had traveled from the Black Sea to the Red Sea; and it was perhaps in one of Tigran’s or Mithridates’ palaces that this apron had been taken. After what we said above, it seems natural to think that this golden ball, undoubtedly carried on a foot in the middle of the apron, was the astronomical representation of the game, that is to say a celestial sphere, on which the planets were to be marked, as well as the twelve signs of the zodiac.
If it is only a conjecture, it is not at least not without some probability. It fits moreover very well in the order of the ideas which we developed previously; and it is with this that we will end what we had to say about the game of twelve lines.
Footnotes
- English translations of the rules of trictrac: https://bkgm.com/variants/Trictrac.html https://booksongaming.com/trictrac/rules/index.htm
- https://fr.wikipedia.org/wiki/Trictrac